Label Leaking in Adversarial Training

What is Label Leaking Effect?

Label leaking effect, is the phenomenon that during adversarial training, the validation error on adversarial examples are smaller than the validation error on clean examples. The effect is reported in this paper, and it is an interesting one. Adversarial examples are supposed to confuse the neural nets during training so as to increase the robustness. It is like a form of data augmentation, and it is supposed to increase the difficulty for neural nets to success. Nevertheless, at the end of training, models are able to solve the problem of classifying adversarial examples better than the original problem.

The problem is that when one uses one-step methods that involves the true labels to craft adversarial samples, there is extra information about label being leaked, thus making the problem simple. To see how it works, let’s start by examine one such method, Fast Gradient Sign Method (FGSM).

How Does FGSM Leak Label Information?

Suppose we have original data $X,Y_{true}$ and a model $F$ . Our prediction is $Y_{pred} = F(X)$. Our loss function is $L(Y_{true}, Y_{pred})$ telling us how far $Y_{pred}$ is away from $Y_{true}$. In FGSM, the motivation is to increase the loss by add to $X$ a small perturbation which is proportional to the sign of the gradient of $L$ w.r.t. $X$. That is $$ X_{adv} = X + \epsilon sign( \frac{\partial L(Y_{true}, Y_{pred})}{\partial X} ) $$ where $X_{adv}$ is called the adversarial sample, and $\epsilon$ controls the step size. In the case of image-classification, we could further add some details. That is $$ output = f(X) $$ $$ Y_{pred} = SoftMax(output) $$ $$ L(Y_{true}, Y_{pred}) = CrossEntropy(Y_{true}, Y_{pred}) $$

Then we have $$ \frac{\partial L(Y_{true}, Y_{pred})}{\partial X}=\frac{\partial L(Y_{true}, Y_{pred})}{\partial output} \frac{\partial output}{\partial X}=(Y_{pred}-Y_{true})\frac{\partial output}{\partial X} $$ For different $X$, the part of $\frac{\partial output}{\partial X}$ is dominated by a big product of weight matrix and activations. For two images with the same label, their activations in any fixed networks are close, and the weights of the network are fixed. As a result $\frac{\partial output}{\partial X}$ is almost a constant for $X$ with the same label. That means, the resulting gradient is highly correlated with the $Y_{true}$, and therefore the label information is leaked in this gradient term.

As a result, when added the gradient, classifying $X_{adv}$ could become a simpler problem than the original problem of classifying $X$, as $X_{adv}$ contains extra information from the added gradient.

I did an experiment on MNIST. The original model is a three layer MLP with random initialization. After extract the sign of the gradients, I further transform each gradient between 0 and 1 by $$ X_{noise} = clip(gradient+1, 0, 1) $$ I fit a simple linear model on the dataset $X_{noise}, Y_{true}$ using SGD without any careful tuning. As a result, I obtained a $96%$ validation error. This confirms the hypothesis.

If classifying $X_{adv}$ becomes a easier problem, then one can imagine that when doing training by adding adversarial samples, the network would find a weight configuration such that it fully take advantage of the extra label information hidden in the label. If the difficulty gap between the original $X$ and $X_{adv}$ is too large, then it is expected that the validation error on the adversarial samples are lower. That’s why we don’t observe label leaking effect on MNIST but only on ImageNet, since classifying $X$ is easy enough.

Label Leaking in Cifar-10

To further illustrate this effect, I use FGSM to adversarial train a resNet with 110 layers on Cifar10, since no one has tried to reproduce this effect on cifar yet. The adversarial training process is the same as here. I replaced half of the batch with adversarial samples, with $\epsilon \sim N(\mu=0, \sigma=12)$, and I discarded the negative $\epsilon$ sampled. During evaluation, I set $\epsilon$ to be 6. After carefully tuning the learning rate and momentum, I obtain validation accuracy on clean and adversarial examples to be respectively $92.12%$ and $94.81%$. Boom, mission completed.

In order to further appreciate this effect, I also provide the cross entropy vs $\epsilon$ graph on the validation data. By varying the $\epsilon$ along the direction along which the loss increases fastest, we could find some interesting insight about why adversarial training work.

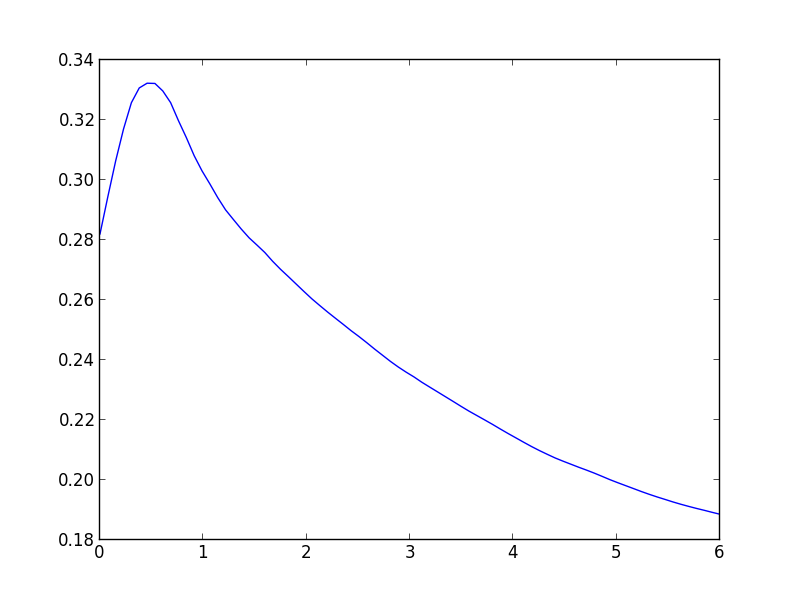
• With increasing $\epsilon$, the loss first increases. This is understandable since gradient is the direction along which the loss increases fastest.
• After a peak, the loss start decreasing. This is the gradient masking effect of adversarial training, as is also reported in Figure 2 of this paper. We can also see at $\epsilon=6$, the loss is even lower than $\epsilon=0$, which is consistent with the label leaking effect we observed before.
• This is graph also illustrate why adversarial training using one-step FGSM cannot defend attacks from iterative FGSM. In iterative methods, the attacker could still follow the curve and find that little peak to fool the network.

Conclusion

Label leaking effect is an counter-intuitive phenomenon, since we are expecting that adversarial samples are a form of data augmentation, and thus are harder problems to solve. After these experiments, I believe this effect is caused by the correlation between the added noise and true label, and this effect would occur only when the original classification problem is very hard.

One more question is if we can avoid this by using least-likely class when calculating the gradients, I personally don’t think that it can solve the problem. Because even if we are not using the true label, for images in the same class, they might have the same least-likely class label, because of the same reason that they have similar activations. As a result, there is still a strong correlation between the gradient and the true label, because of the strong correlation between the least-likely label and the true label. Nevertheless, further experiment could be done to prove or disprove this.